Пряма
Пряма́ — одне з основних понять геометрії. При систематичному викладі геометрії пряма лінія зазвичай приймається за одне з вихідних понять, яке лише опосередковано визначається аксіомами геометрії. Якщо основою побудови геометрії служить поняття відстані між двома точками простору, то пряму лінію можна визначити як лінію, шлях уздовж якої дорівнює відстані між двома точками. Основна властивість прямої: через будь-які дві точки можна провести пряму, і до того ж тільки одну. Алгебраїчне визначення[ред. • ред. код]
Три графіки лініній — червона та синя мають однаковий нахил k, а червона та зелена мають однаковий зсув b.
[[|міні|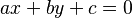 ]]
де a\,, b\,, c\, — деякі числа, при чому a\, або b\, повинне бути відмінне від нуля.[1] Це рівняння - загальне рівняння прямої. Його також називають «стандартним».
Натомість, Канонічне рівняння прямої, що випливає з попереднього має вигляд лінійної функції:
[[|міні|
]]
де a\,, b\,, c\, — деякі числа, при чому a\, або b\, повинне бути відмінне від нуля.[1] Це рівняння - загальне рівняння прямої. Його також називають «стандартним».
Натомість, Канонічне рівняння прямої, що випливає з попереднього має вигляд лінійної функції:
[[|міні|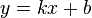 ]]
]]
Пряма (а також пара пересічних прямих) є виродженим прикладом конічного перетину. В n-вимірному просторі[ред. • ред. код] Нехай задано вектор k в n-вимірному Евклідовому просторі E^n, k = (k_i) \in E^n, та \alpha_1, \dots, \alpha_n — деякі фіксовані числа. Геометричне місце точок x=x_i простору E^n, координати яких представлено у вигляді:
x_i = k_i + \alpha_i t,\qquad -\infty< t < +\infty,\quad i=1, \dots, n,
називається прямою в просторі E^n що проходить через точку k в «напрямі» (\alpha_1, \dots, \alpha_n).[2]
Частина прямої, що відповідає зміні параметру t в деякому відрізку [a, b] називається прямолінійним відрізком а її частина, що відповідає зміні параметру в проміжку t\ge a, — промінем.
Якщо задано дві точки (x'_i), (x_i) то рівняння прямої, що проходить через ці точки матиме вигляд:
[[|міні|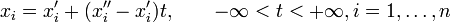 ]]
[[|міні|
]]
[[|міні|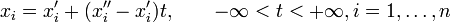 ]]
]]