Відмінності між версіями «Дифузія»

Версія за 16:19, 22 листопада 2018

Дифу́зія (лат. diffusio — поширення, розтікання, розсіювання, взаємодія) — процес взаємного проникнення молекул або атомів однієї речовини поміж молекул або атомів іншої, що зазвичай приводить до вирівнювання їх концентрацій у всьому займаному об'ємі.

У деяких ситуаціях одна з речовин уже має вирівняну концентрацію, і говорять про дифузію одної речовини в іншій. При цьому зазвичай перенесення речовини відбувається з області з високою концентрацією в область з низькою концентрацією (вздовж вектора градієнта концентрації).

Прикладом дифузії може служити перемішування газів (наприклад, поширення запахів) або рідин (якщо у воду капнути чорнила, то рідина через деякий час стане рівномірно пофарбованою). Інший приклад пов'язаний з твердим тілом: атоми дотичних металів перемішуються на кордоні дотику. Важливу роль дифузія частинок грає у фізиці плазми.

Зазвичай під дифузією розуміють процеси, що супроводжуються переносом речовини, однак іноді дифузійними називають також інші процеси перенесення: теплопровідність, в'язке тертя тощо.

Швидкість протікання дифузії залежить від багатьох факторів. Так, у разі металевого стрижня дифузія тепла проходить дуже швидко. Якщо ж стрижень виготовлений з синтетичного матеріалу, дифузія тепла протікає повільно. Дифузія молекул в загальному випадку протікає ще повільніше. Наприклад, якщо шматочок цукру опустити на дно склянки з водою, і воду не перемішувати, то пройде кілька тижнів, перш ніж розчин стане однорідним. Ще повільніше відбувається дифузія однієї твердої речовини в іншу. Наприклад, якщо мідь покрити золотом, то буде відбуватися дифузія золота в мідь, але при нормальних умовах (кімнатна температура і атмосферний тиск) золотовмісний шар досягне товщини в кілька мікронів тільки через кілька тисяч років. Інший приклад: на золотий злиток був покладений злиток свинцю, і під вантажем за п'ять років свинцевий злиток проникнув в золотий злиток на сантиметр.

Кількісно опис процесів дифузії було дано німецьким фізіологом Адольфом Фіком в 1855 р.

Загальна інформація

Дифузія — одна із ступенів численних технологічних процесів фізичної хімї(адсорбції, сушки, екстрагування, брикетування зі зв'язуючими тощо). Дифузія відбувається в газах, рідинах і твердих тілах. Механізм дифузії в цих речовинах істотно різний. Дифузія що відбувається внаслідок теплового руху атомів, молекул, — молекулярна дифузія. Дифундувати можуть як частинки сторонніх речовин (домішок), нерівномірно розподілених у середовищі, так і частинки самої речовини середовища. У останньому випадку процес називається самодифузією. Термодифузія — це дифузія під дією градієнта температури в об'ємі тіла, бародифузія — під дією градієнта тиску або гравітаційного поля. Перенесення заряджених частинок під дією зовнішнього електричного поля — електродифузія. У рухомому середовищі може виникати конвекційна дифузія, при вихровому русі газу або рідини — турбулентна дифузія.

Наслідком дифузії є переміщення часток із областей, де їхня концентрація висока, в області, де їхня концентрація низька, тобто вирівнювання концентрації часток у термодинамічній системі, встановлення рівноваги за складом.

Дифузія дуже розповсюджене явище, яке відіграє велику роль у функціонуванні живих організмів. У легенях молекули кисню дифундують у кровоносні судини, завдяки процесам дифузії відбувається обмін речовин у клітинах.

Дифузія широко використовується у техніці. Наприклад, робота біполярного транзистора основана на дифузії неосновних носіїв заряду через p-n перехід. Вибіркове перенесення певних компонентів у пори речовини — інфільтраційна дифузія. Дифузія має особливе значення в шахтах, де вона сприяє рівномірному розподілу шкідливих газів в атмосфері гірн. виробок, попередженню їх небезпечних скупчень. Суттєве значення відіграє дифузія в технологічних процесах при застосуванні реагентів. Різні речовини дифундують з різною швидкістю, що залежить від молекулярної маси речовини. Цей факт використовується для розділення ізотопів.

У загальному випадку можна сказати, що темп дифузії пропорційний швидкості молекул (яка, в свою чергу, пропорційна температурі і обернено пропорційна масі молекул), а також пропорційний площі перерізу зразка.

Ілюстрації

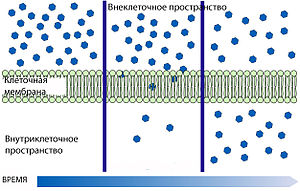
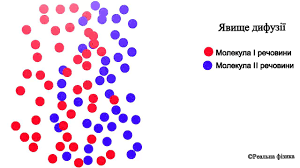
Математичний опис

Джерела та література

Зовнішні посилання

@@ Рядок 33: / Рядок 33: @@
 ==Математичний опис==
-Дифузійний потік
-Дифузійним потоком або густиною дифузійного потоку j називають кількість речовини, що проходить через одиницю площі за одиницю часу. Ця величина дорівнює
-{\displaystyle \mathbf {j} =-D\nabla n} {\displaystyle \mathbf {j} =-D\nabla n}.
-тобто, потік пропорційний градієнту концентрації (перший закон Фіка). Знак мінус показує, що дифузія відбувається у напрямку, протилежному до зростання градієнту. Величина {\displaystyle D} D називається коофіцієнтом дифузії, і є мірою дії середовища на частинки. Фізичний сенс коофіцієнта дифузії: це кількість речовини, що проходить через ділянку в 1 м2 при градієнті концентрації речовини у 1 моль/м3 на метр.
-Рівняння дифузії
-З рівняння неперервності (яке можна розуміти як закон збереження кількості частинок) можна вивести рівняння дифузії
-{\displaystyle {\frac {\partial n}{\partial t}}+{\text{div}}\,\mathbf {j} =0} {\displaystyle {\frac {\partial n}{\partial t}}+{\text{div}}\,\mathbf {j} =0}
-а використавши вираз для густини потоку, можна отримати феноменологічне рівняння дифузії
-{\displaystyle {\frac {\partial n}{\partial t}}={\text{div}}D\nabla n} {\displaystyle {\frac {\partial n}{\partial t}}={\text{div}}D\nabla n},
-що у випадку незмінного D перетворюється на другий закон Фіка:
-{\displaystyle {\frac {\partial n}{\partial t}}=D\Delta n} {\displaystyle {\frac {\partial n}{\partial t}}=D\Delta n},
-де {\displaystyle \Delta ={\text{div}}\,\nabla } {\displaystyle \Delta ={\text{div}}\,\nabla } — оператор Лапласа.[1]
-У більш загальному випадку систем часток, які взаємодіють між собою рівняння дифузії записується у вигляді:
-{\displaystyle {\frac {\partial n}{\partial t}}={\text{div}}\,(Dn\nabla \mu )+f(x,t)} {\displaystyle {\frac {\partial n}{\partial t}}={\text{div}}\,(Dn\nabla \mu )+f(x,t)} ,
-де μ — хімічний потенціал а f — інтенсивність джерел речовини. Це рівняння виражає той факт, що умовою рівноваги за складом є рівність хімічного потенціалу у всій термодинамічній системі, а вирівнювання концентрації — це лише частковий випадок для однорідних систем, близьких до ідеального газу.
-У найпростішому випадку розглядається одновимірна система з початковою концентрацією заданою дельта-функцією[2], що відповідає одноразовому миттєвому внесенню дифундуючої речовини у середовище (наприклад, крапля чорнил, що потрапляє всередину трубки з водою)
-{\displaystyle n(r,t)={\frac {1}{\sqrt {4\pi Dt}}}e^{-{\frac {x^{2}}{4Dt}}}} {\displaystyle n(r,t)={\frac {1}{\sqrt {4\pi Dt}}}e^{-{\frac {x^{2}}{4Dt}}}}
-У випадку довільної початкової функції {\displaystyle \phi (x)} {\displaystyle \phi (x)},
-{\displaystyle n(x,t)=\int _{-\infty }^{\infty }G(x,\xi ,t)\phi (\xi )d\xi } {\displaystyle n(x,t)=\int _{-\infty }^{\infty }G(x,\xi ,t)\phi (\xi )d\xi }, де
-{\displaystyle G(x,\xi ,t)={\frac {1}{\sqrt {4\pi Dt}}}e^{-{\frac {(x-\xi )^{2}}{4Dt}}}} {\displaystyle G(x,\xi ,t)={\frac {1}{\sqrt {4\pi Dt}}}e^{-{\frac {(x-\xi )^{2}}{4Dt}}}}
-де <math}\xi</math> — поточна координата інтегрування. Таке рівняння називається фундаментальним розв'язком рівняння диффузії при заданих початкових умовах.
-Більш складні випадки включають коофіцієнт дифузії, що залежить від часу, температури або концентрації дифундуючої речовини, змінну геометрію середовища, хімічні реакції між речовиною і середовищем, тощо. [3]З математичної точки зору, рівняння дифузії є частковим випадком рівняння Нав'є — Стокса. Також, у загальному вигляді, вони є аналогічними рівнянням теплопровідності.
-Випадкові блукання
-При диффузії кожна частинка речовини рухається хаотично під дією оточуючих її частинок. Цей рух є аналогічним броунівському, а тому має аналогічні характеристики. Для частки характерна пропорційність середнього зміщення квадратному кореню з часу.
-{\displaystyle \langle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}\rangle \propto t} {\displaystyle \langle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}\rangle \propto t},
-де {\displaystyle x} x, {\displaystyle y} y, {\displaystyle z} z — координати частки в момент часу t, {\displaystyle x_{0}} x_0, {\displaystyle y_{0}} {\displaystyle y_{0}}, {\displaystyle z_{0}} {\displaystyle z_{0}} — її коорднати в початковий момент часу. Це спідввідношення дозволяє ввести кількісну характеристику дифузії — коефіцієнт дифузії D:
-{\displaystyle D={\frac {1}{6t}}\langle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}\rangle } {\displaystyle D={\frac {1}{6t}}\langle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}\rangle }.
-==Див. також==
 ==Джерела та література==

Відмінності між версіями «Дифузія»

Версія за 16:19, 22 листопада 2018

Зміст

Загальна інформація

Ілюстрації

Математичний опис

Джерела та література

Зовнішні посилання

Навігаційне меню

Особисті інструменти

Простори назв

Варіанти

Перегляди

Дії

Пошук

Навігація

Інструменти