Відмінності між версіями «Й»
| (не показані 9 проміжних версій ще одного учасника) | |||
| Рядок 15: | Рядок 15: | ||
{| style="width:100%; margin-top:2em; vertical-align:top; border-top:5px #66CDAA solid; border-bottom:5px #66CDAA solid; text-align:center" | {| style="width:100%; margin-top:2em; vertical-align:top; border-top:5px #66CDAA solid; border-bottom:5px #66CDAA solid; text-align:center" | ||
|- valign="top" | |- valign="top" | ||
| − | |style="width:20%; padding-top:1em;"| [[Зображення: | + | |style="width:20%; padding-top:1em;"| [[Зображення:30235_html_m48a68c65.gif|x140px]] |
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| + | |||
==Медіа== | ==Медіа== | ||
==Див. також== | ==Див. також== | ||
| + | |||
| + | -[http://uk.wikipedia.org/wiki/%D0%90%D0%BA%D1%81%D1%96%D0%BE%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0_%D1%82%D0%B5%D0%BE%D1%80%D1%96%D1%97_%D0%B9%D0%BC%D0%BE%D0%B2%D1%96%D1%80%D0%BD%D0%BE%D1%81%D1%82%D0%B5%D0%B9 Аксіоматика теорії ймовірностей] | ||
| + | [http://uk.wikipedia.org/wiki/%D0%A7%D0%B0%D1%81%D1%82%D0%BE%D1%82%D0%B0_%D0%BF%D0%BE%D0%B4%D1%96%D1%97 -Частота події] | ||
| + | [http://uk.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%BD%D0%B0_%D0%B9%D0%BC%D0%BE%D0%B2%D1%96%D1%80%D0%BD%D1%96%D1%81%D1%82%D1%8C -Геометрична ймовірність] | ||
| + | [http://uk.wikipedia.org/wiki/%D0%93%D1%83%D1%81%D1%82%D0%B8%D0%BD%D0%B0_%D1%96%D0%BC%D0%BE%D0%B2%D1%96%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%96 -Густина імовірності] | ||
| + | [http://uk.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%BF%D0%BE%D0%B2%D0%BD%D0%BE%D1%97_%D0%B9%D0%BC%D0%BE%D0%B2%D1%96%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%96 -Формула повної ймовірності] | ||
| + | [http://uk.wikipedia.org/wiki/%D0%A3%D0%BC%D0%BE%D0%B2%D0%BD%D0%B0_%D0%B9%D0%BC%D0%BE%D0%B2%D1%96%D1%80%D0%BD%D1%96%D1%81%D1%82%D1%8C -Умовна ймовірність] | ||
| + | [http://uk.wikipedia.org/wiki/%D0%90%D0%BC%D0%BF%D0%BB%D1%96%D1%82%D1%83%D0%B4%D0%B0_%D0%B9%D0%BC%D0%BE%D0%B2%D1%96%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%96 -Амплітуда ймовірності] | ||
==Джерела та література== | ==Джерела та література== | ||
| + | [http://uk.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BB%D0%BC%D0%BE%D0%B3%D0%BE%D1%80%D0%BE%D0%B2_%D0%90%D0%BD%D0%B4%D1%80%D1%96%D0%B9_%D0%9C%D0%B8%D0%BA%D0%BE%D0%BB%D0%B0%D0%B9%D0%BE%D0%B2%D0%B8%D1%87 Колмогоров А.Н.] (1974). Основные понятия теории вероятностей (вид. 2). Москва: Наука. с. 119. | ||
| + | В. Е. Гмурман. Теория вероятностей и математическая статистика. Издание четвертое, дополненное. М. 1972 | ||
==Зовнішні посилання== | ==Зовнішні посилання== | ||
| + | [http://www.math.uah.edu/stat/ Virtual Laboratories in Probability and Statistics (University of Alabama in Huntsville) (Віртуальна лабораторія імовірності і статистики)] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| − | [[Категорія:Словник Грінченка і сучасність/ | + | [[Категорія:Словник Грінченка і сучасність/Гуманітарний інститут]] |
Поточна версія на 17:51, 30 листопада 2013
Й,Ймові́рність (лат. probabilitas, англ. probability) — числова характеристика можливості того, що випадкова подія відбудеться в умовах, які можуть бути відтворені необмежену кількість разів. Імовірність є основним поняттям розділу математики, що називається теорія імовірностей.
Випадковою подією називається подія, результат якої не може бути відомий наперед. Навіть у тому разі, коли насправді подія детермінована своїми передумовами, вплив цих передумов може бути настільки складним, що вивести з них наслідок логічно й послідовно, неможливо. Наприклад, при підкидуванні монети, сторона на яку монета впаде визначається положенням руки і монети в руці, швидкістю, обертовим моментом тощо, однак відслідкувати всі ці фактори неможливо, тому результат можна вважати випадковим.
Існують два підходи до означення імовірності: математично-аксіоматичний і Баєсів. Аксіоматичний підхід, строго сформульований Колмогоровим, будується на припущенні, що імовірності елементарних випадкових подій задані, і зосереджується на визначенні ймовірностей складних подій, що є сукупністю елементарних. Так, наприклад, при підкидуванні шестигранного кубика гральної кості, ймовірності випадіння будь-якого числа, вважаються однаковими й рівними 1/6. Виходячи з цієї аксіоми, теорія ймовірності може розрахувати ймовірність того, що сума чисел на двох костях буде, наприклад, 8.
Баєсів підхід не робить припущень про ймовірності елементарних подій, а намагається отримати їх із аналізу попереднього досвіду, спираючись на теорему Баєса і на попередні гіпотези. Баєсів підхід ближчий до того, як визначаються імовірності випадкових подій у природознавстві. Оскільки ці ймовірності наперед невідомі, результати серії дослідів розбиваються на сприятливі й несприятливі, і експериментально визначена ймовірність дорівнює відношенню числа сприятливих подій до числа дослідів, тобто частоті подій.
Надалі в цій статті використовується аксіоматичний математичний підхід. сз. = І, сз. (см.).
Зміст
Сучасні словники
Тлумачення слова у сучасних словниках
Ілюстрації
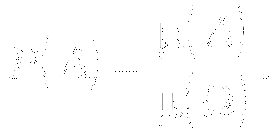
|
Медіа
Див. також
-Аксіоматика теорії ймовірностей -Частота події -Геометрична ймовірність -Густина імовірності -Формула повної ймовірності -Умовна ймовірність -Амплітуда ймовірності
Джерела та література
Колмогоров А.Н. (1974). Основные понятия теории вероятностей (вид. 2). Москва: Наука. с. 119. В. Е. Гмурман. Теория вероятностей и математическая статистика. Издание четвертое, дополненное. М. 1972