Відмінності між версіями «Лісова Людмила Юріївна-ПВ(ф)»
| (не показано 15 проміжних версій цього учасника) | |||
| Рядок 1: | Рядок 1: | ||
=='''Використання ЕНК на уроках математики як засобу підготовки до ЗНО'''== | =='''Використання ЕНК на уроках математики як засобу підготовки до ЗНО'''== | ||
| − | '''Постановка проблеми.''' Не викликає сумнівів актуальність удосконалення методики підготовки до зовнішнього незалежного оцінювання (ЗНО) навчальних досягнень українських випускників. Цей тип національного стандартизованого оцінювання в Україні постійно перебуває у центрі уваги як фундаментальних досліджень (див. (Дворецька, 2015), (Ляшенко та Раков, 2008), (Іяковлєва та Каплун, 2019) та ін.), так і публікацій у ЗМІ (див. (Рейтинг Груп Україна, 2018), (НаУрок, 2021), (Швадчак, 2021) тощо).Водночас ставлення до ЗНО загалом і до ЗНО з математики зокрема в українському суспільстві в цілому позитивне. | + | '''Постановка проблеми.''' Організація дистанційного навчання для здобувачів освіти в Україні набула особливого значення у зв’язку з викликами, що поставили перед українським суспільством спочатку пандемія Сovid-19, а останні півроку російсько-українська війна. Вже три роки навчання в Україні, а отже, значна частина життя перейшла в цифровий світ. ІКТ, ЕНК, сучасні е-ресурси, інтернет мережа надають можливість проводити навчальний процес, зокрема допомагати у підготовці до ЗНО, при цьому не втрачаючи якості навчання. |
| + | |||
| + | Не викликає сумнівів актуальність удосконалення методики підготовки до зовнішнього незалежного оцінювання (ЗНО) навчальних досягнень українських випускників. Цей тип національного стандартизованого оцінювання в Україні постійно перебуває у центрі уваги як фундаментальних досліджень (див. (Дворецька, 2015), (Ляшенко та Раков, 2008), (Іяковлєва та Каплун, 2019) та ін.), так і публікацій у ЗМІ (див. (Рейтинг Груп Україна, 2018), (НаУрок, 2021), (Швадчак, 2021) тощо).Водночас ставлення до ЗНО загалом і до ЗНО з математики зокрема в українському суспільстві в цілому позитивне. | ||
Наприклад, опитування понад 700 користувачів (учнів, їхніх батьків та вчителів математики) освітньої платформи GIOS [2] показує, що середній бал якості ЗНО з математики в Україні за 10-бальною шкалою (1 – найнижчий рівень задоволеності, 10 – найвищий) дорівнює 7, а найпопулярніше значення цієї якості – 8. Серед найбільших переваг незалежного оцінювання часто називають: зменшення корупції під час вступу до університетів (42% респондентів), можливість об’єктивно оцінити рівень навчальних досягнень учнів з математики (28%), можливість ширшого вибору навчальних закладів під час вступної кампанії (26%) та підвищення престижу вивчення математики в школі (18). %). | Наприклад, опитування понад 700 користувачів (учнів, їхніх батьків та вчителів математики) освітньої платформи GIOS [2] показує, що середній бал якості ЗНО з математики в Україні за 10-бальною шкалою (1 – найнижчий рівень задоволеності, 10 – найвищий) дорівнює 7, а найпопулярніше значення цієї якості – 8. Серед найбільших переваг незалежного оцінювання часто називають: зменшення корупції під час вступу до університетів (42% респондентів), можливість об’єктивно оцінити рівень навчальних досягнень учнів з математики (28%), можливість ширшого вибору навчальних закладів під час вступної кампанії (26%) та підвищення престижу вивчення математики в школі (18). %). | ||
| Рядок 7: | Рядок 9: | ||
Сильним стимулом для розвитку ІКТ у навчанні математики також стала нинішня воєнна та попередня пандемічна ситуація, коли запровадження карантину та тривалі періоди онлайн-навчання вже сприймаються і учнями, і вчителями як цілком нормальні навчальні ситуації. За цих обставин вчителі та репетитори математики часто просто змушені використовувати ІКТ, створювати та розвивати нові форми організації навчального процесу, удосконалювати та відповідно адаптувати методики та технології навчання. | Сильним стимулом для розвитку ІКТ у навчанні математики також стала нинішня воєнна та попередня пандемічна ситуація, коли запровадження карантину та тривалі періоди онлайн-навчання вже сприймаються і учнями, і вчителями як цілком нормальні навчальні ситуації. За цих обставин вчителі та репетитори математики часто просто змушені використовувати ІКТ, створювати та розвивати нові форми організації навчального процесу, удосконалювати та відповідно адаптувати методики та технології навчання. | ||
| − | '''Мета статті:''' з’ясувати доцільність використання | + | '''Мета статті:''' з’ясувати доцільність використання ЕНК, а також як місце і роль технологій у підготовці до ЗНО з математики з позиції тих, хто цю підготовку здійснює (вчителів, репетиторів тощо); визначити, наскільки сучасні технології сприяють чи перешкоджають пошуку оптимальних методів підготовки до незалежного тестування з математики; окреслити шляхи розробки методичних рекомендацій щодо використання ЕНК при підготовці до ЗНО з математики. |
'''Матеріали та методи дослідження''' Для досягнення поставленої мети використано теоретичний метод аналізу методичної літератури з досліджуваного питання. Також я використовую деякі емпіричні методи: власне опитування за допомогою електронного інструменту Google form, спостереження за навчальним процесом у загальноосвітніх школах та на курсах підготовки до спеціальних іспитів, а також аналіз досягнень учнів. У цій статті я також використовую комплекс методів наукового пізнання: порівняльний аналіз для з’ясування різних поглядів на проблему та визначення напрямків дослідження; систематизація та узагальнення з метою висновків і формулювання рекомендацій щодо підготовки до загальнодержавного стандартизованого оцінювання навчальних досягнень з математики; узагальнення педагогічного досвіду та спостережень. | '''Матеріали та методи дослідження''' Для досягнення поставленої мети використано теоретичний метод аналізу методичної літератури з досліджуваного питання. Також я використовую деякі емпіричні методи: власне опитування за допомогою електронного інструменту Google form, спостереження за навчальним процесом у загальноосвітніх школах та на курсах підготовки до спеціальних іспитів, а також аналіз досягнень учнів. У цій статті я також використовую комплекс методів наукового пізнання: порівняльний аналіз для з’ясування різних поглядів на проблему та визначення напрямків дослідження; систематизація та узагальнення з метою висновків і формулювання рекомендацій щодо підготовки до загальнодержавного стандартизованого оцінювання навчальних досягнень з математики; узагальнення педагогічного досвіду та спостережень. | ||
| − | '''Виклад основного матеріалу''' | + | '''Виклад основного матеріалу''' У ЗНО з математики передбачається перевірка навчальних досягнень випускників з програмового матеріалу за 5 - 11 класи. Така перевірка використовує педагогічний тест. Згідно з [7] «педагогічний тест ... – це набір завдань з певної галузі знань (навчального предмета), побудованих за певними правилами викладу умови і надання відповіді, за допомогою яких оцінюється рівень навчальних досягнень учнів (знання, вміння, предметна компетентність тощо)». |
| − | На мою думку, незалежне оцінювання є лише інструментом адекватного оцінювання рівня навчальних досягнень учнів, своєрідною «лінійкою», яка призначена лише для «вимірювання» і не більше того. Для мене також очевидно, що ЗНО з математики чи будь-якого іншого предмету не має бути метою шкільного навчання. Головною метою навчання в школі є розвиток дитини, виявлення і розкриття її здібностей, а також формування тих життєвих компетентностей, які дозволять їй у майбутньому знайти своє місце в житті, реалізуватися як особистості. І незалежне тестування, хоч і є класичним «високим тестуванням» | + | Хоча педагогічне тестування має багато недоліків, але воно дає змогу: |
| + | |||
| + | • перевірити результати навчальних досягнень водночас із багатьох тем і розділів програми; | ||
| + | |||
| + | • об’єктивно оцінити рівень засвоєння навчального матеріалу; | ||
| + | |||
| + | • створити для всіх учасників тестування рівні умови складання тестів; | ||
| + | |||
| + | • стандартизувати та автоматизувати процедуру перевірки результатів; | ||
| + | |||
| + | • охопити тестуванням велику кількість учнів [3]. | ||
| + | |||
| + | Зрозуміло, що не існує універсальної методики підготовки до ЗНО з математики, яка б гарантувала високий бал кожному учаснику тестування. Дійсно, це суттєво залежить від студентської аудиторії та індивідуальних особливостей викладача чи репетитора, який його здійснює. Перш за все, слід говорити про комплекс методів, які дозволять сучасному вчителю математики досягти бажаного результату, який, у свою чергу, залежить від мети підготовки до ЗНО. Зупинимося на цьому питанні докладніше. | ||
| + | |||
| + | На мою думку, незалежне оцінювання є лише інструментом адекватного оцінювання рівня навчальних досягнень учнів, своєрідною «лінійкою», яка призначена лише для «вимірювання» і не більше того. Для мене також очевидно, що ЗНО з математики чи будь-якого іншого предмету не має бути метою шкільного навчання. Головною метою навчання в школі є розвиток дитини, виявлення і розкриття її здібностей, а також формування тих життєвих компетентностей, які дозволять їй у майбутньому знайти своє місце в житті, реалізуватися як особистості. І незалежне тестування, хоч і є класичним «високим тестуванням» [11], саме по собі не може стати кінцевою метою чи викладання кожної дисципліни, чи навіть вказівка до створення методики навчання. | ||
Тому я вважаю, що основною метою вчителя при підготовці до ЗНО з математики є повторення та систематизація даних зі шкільного курсу математики, а не формальне привчання учнів до цілком конкретних класів тестових завдань. Звичайно, необхідно адаптувати випускників до особливостей розв’язування тестових завдань різної форми (з альтернативою, з короткою відповіддю, на встановлення відповідності, з повним поясненням), але ця мета є другорядною і не може витіснити чи замінити основну. | Тому я вважаю, що основною метою вчителя при підготовці до ЗНО з математики є повторення та систематизація даних зі шкільного курсу математики, а не формальне привчання учнів до цілком конкретних класів тестових завдань. Звичайно, необхідно адаптувати випускників до особливостей розв’язування тестових завдань різної форми (з альтернативою, з короткою відповіддю, на встановлення відповідності, з повним поясненням), але ця мета є другорядною і не може витіснити чи замінити основну. | ||
| − | Також важливою при підготовці до ЗНО з математики є мета, яку ставить перед собою майбутній учасник цього ЗНО. З першого погляду видно, що студент хоче набрати якомога більше балів. Однак такий підхід може мати серйозні негативні наслідки в майбутньому. На мою думку, більш природним є те, що учні під час підготовки до ЗНО намагаються отримати не максимальний, а «свій» бал, тобто такий, який адекватно відображатиме реальний рівень підготовки і дозволить здавати «своє» місце за обраною спеціальністю в університеті. Таке цілепокладання дозволить випускнику уникнути значних психологічних проблем під час підготовки до тестування, а також з часом знайти ту спеціальність і університет, які дозволять йому стати реалізованою та щасливою людиною (детальніше про це див. у статті [ | + | Також важливою при підготовці до ЗНО з математики є мета, яку ставить перед собою майбутній учасник цього ЗНО. З першого погляду видно, що студент хоче набрати якомога більше балів. Однак такий підхід може мати серйозні негативні наслідки в майбутньому. На мою думку, більш природним є те, що учні під час підготовки до ЗНО намагаються отримати не максимальний, а «свій» бал, тобто такий, який адекватно відображатиме реальний рівень підготовки і дозволить здавати «своє» місце за обраною спеціальністю в університеті. Таке цілепокладання дозволить випускнику уникнути значних психологічних проблем під час підготовки до тестування, а також з часом знайти ту спеціальність і університет, які дозволять йому стати реалізованою та щасливою людиною (детальніше про це див. у статті [10, 11]. |
Після узгодження цілей підготовки до ЗНО для учня та вчителя природним наступним кроком є вибір відповідної методики систематизації та повторення шкільної математики. Як уже зазначалося, цей вибір залежить від багатьох факторів, але сьогодні, після більш ніж 15-річної історії, набір таких методик уже сформовано та відображено в різних посібниках для підготовки до незалежного оцінювання ((Бевз та Буковська, 2020), (Гальперіна, 2020), (Капіносов, 2020), (Нелін, 2016), (Роганін, 2020), (Захарійченко та ін., 2020), Захарійченко та ін., 2021)). Кожна з цих книг має свою внутрішню логіку, послідовність вивчення тем, свої переваги та недоліки. | Після узгодження цілей підготовки до ЗНО для учня та вчителя природним наступним кроком є вибір відповідної методики систематизації та повторення шкільної математики. Як уже зазначалося, цей вибір залежить від багатьох факторів, але сьогодні, після більш ніж 15-річної історії, набір таких методик уже сформовано та відображено в різних посібниках для підготовки до незалежного оцінювання ((Бевз та Буковська, 2020), (Гальперіна, 2020), (Капіносов, 2020), (Нелін, 2016), (Роганін, 2020), (Захарійченко та ін., 2020), Захарійченко та ін., 2021)). Кожна з цих книг має свою внутрішню логіку, послідовність вивчення тем, свої переваги та недоліки. | ||
| Рядок 25: | Рядок 41: | ||
Однак у зв’язку з пандемічною ситуацією та запровадженням карантину після 2020 року ситуація суттєво змінилася, оскільки заняття в аудиторіях стали неможливими. Студентам і викладачам довелося фактично терміново освоювати засоби дистанційного спілкування (Google Meet, Skype, Zoom та ін.) та платформи для дистанційного та змішаного навчання (Google Classroom, MS Teams, MOODLE, НаУрок та ін.), з за допомогою якого, зокрема, проводились і контрольні заходи у формі комп’ютерного тестування. | Однак у зв’язку з пандемічною ситуацією та запровадженням карантину після 2020 року ситуація суттєво змінилася, оскільки заняття в аудиторіях стали неможливими. Студентам і викладачам довелося фактично терміново освоювати засоби дистанційного спілкування (Google Meet, Skype, Zoom та ін.) та платформи для дистанційного та змішаного навчання (Google Classroom, MS Teams, MOODLE, НаУрок та ін.), з за допомогою якого, зокрема, проводились і контрольні заходи у формі комп’ютерного тестування. | ||
| − | Описана ситуація призвела до суттєвих змін у сприйнятті ІКТ як студентами, так і викладачами та викладачами. Це підтверджують результати вищезгаданого опитування користувачів освітньої платформи GIOS [2], серед яких 49% респондентів обрали найбільш оптимальним способом підготовки до ЗНО з математики спосіб занять з репетитором за друкованими посібниками. та онлайн-платформи. Проте це опитування не заглиблювалося в деталі та особливості використання вчителями та репетиторами новітніх технологій під час підготовки до ЗНО з математики. Тому я провела власне опитування вчителів математики щодо використання ними | + | Описана ситуація призвела до суттєвих змін у сприйнятті ІКТ як студентами, так і викладачами та викладачами. Це підтверджують результати вищезгаданого опитування користувачів освітньої платформи GIOS [2], серед яких 49% респондентів обрали найбільш оптимальним способом підготовки до ЗНО з математики спосіб занять з репетитором за друкованими посібниками. та онлайн-платформи. Проте це опитування не заглиблювалося в деталі та особливості використання вчителями та репетиторами новітніх технологій під час підготовки до ЗНО з математики. Тому я провела власне опитування вчителів математики щодо використання ними ЕНК під час підготовки учнів до незалежного оцінювання. |
| + | |||
| + | <gallery> | ||
| + | Файл:2023-05-25 10-35-27.png|Рисунок 1 | ||
| + | Файл:2023-05-25 11-41-13.png|Рисунок 2 | ||
| + | </gallery> | ||
Згідно результатів досліження, серед респондентів більше 80% беруть безпосередню участь у підготовці учнів до ЗНО з математики, решта – опосередковано. Дві третини респондентів вважають, що найкращим способом підготовки до ЗНО сьогодні є поєднання аудиторних занять та онлайн-формату. Водночас майже третина вважає, що таке навчання має здійснюватися виключно в аудиторії. Виключно онлайн-формат підготовки до тестування не є популярним з точки зору його ефективності та ефективності. Можна припустити, що перевага на користь комбінованого підходу (аудиторний формат та онлайн-заняття) є наслідком вимушеного активного розвитку та практичного застосування змішаного навчання протягом останнього року. Відповідно, якщо за таких умов роботи та навчання студенти будуть показувати не нижчі результати, ніж за класичних форм роботи, то, швидше за все, ми побачимо ще більший відсоток прихильників комбінованого підходу. Однак можлива й зворотна ситуація, коли перехід від аудиторної роботи до онлайн не виправдає своєї ефективності в очах її нинішніх прихильників | Згідно результатів досліження, серед респондентів більше 80% беруть безпосередню участь у підготовці учнів до ЗНО з математики, решта – опосередковано. Дві третини респондентів вважають, що найкращим способом підготовки до ЗНО сьогодні є поєднання аудиторних занять та онлайн-формату. Водночас майже третина вважає, що таке навчання має здійснюватися виключно в аудиторії. Виключно онлайн-формат підготовки до тестування не є популярним з точки зору його ефективності та ефективності. Можна припустити, що перевага на користь комбінованого підходу (аудиторний формат та онлайн-заняття) є наслідком вимушеного активного розвитку та практичного застосування змішаного навчання протягом останнього року. Відповідно, якщо за таких умов роботи та навчання студенти будуть показувати не нижчі результати, ніж за класичних форм роботи, то, швидше за все, ми побачимо ще більший відсоток прихильників комбінованого підходу. Однак можлива й зворотна ситуація, коли перехід від аудиторної роботи до онлайн не виправдає своєї ефективності в очах її нинішніх прихильників | ||
| − | Зазначу, що 98% респондентів вважають використання | + | Зазначу, що 98% респондентів вважають використання ЕНК доцільним під час підготовки до ЗНО з математики. Так званим «лідером використання» новітніх технологій є онлайн-платформи для тестування (близько 80% респондентів). Причому цей показник приблизно однаковий як серед тих, хто вважає ефективнішим комбінований підхід у навчанні, так і серед тих, хто вважає більш ефективним лише аудиторне навчання. Тобто онлайн-тестування активно використовується і під час роботи на уроці. Також 45% прихильників аудиторного формату навчання та 54% тих, хто обирає комбінований підхід, вважають за доцільне використовувати ІКТ під час підготовки до уроків. |
| + | |||
| + | Цікаво відзначити, що відсоток тих, хто використовує ЕНК для спілкування зі студентами, більш ніж утричі вищий серед тих, хто використовує комбінований підхід, ніж серед тих, хто надає перевагу суто аудиторній роботі. При цьому відсоток тих, хто не має технічної можливості правильно використовувати можливості ЕНК, також втричі вищий серед тих, хто вважає навчання в аудиторному форматі ефективнішим. Таким чином, на прихильність до включення онлайн-формату в процес підготовки до ЗНО з математики значною мірою впливає технічне забезпечення викладача, зокрема, в контексті можливості спілкування зі студентом без живих зустрічей. | ||
| + | |||
| + | Як видно з рисунку 2, серед усіх сучасних технологій, які використовують вчителі математики під час підготовки до ЗНО з математики, лідирують платформи онлайн-тестів (їми користуються майже 80% респондентів). Однак найбільшою проблемою цих платформ є низький рівень рецензування та перевірки їхніх матеріалів, оскільки переважну більшість тестів на цих платформах пишуть самі викладачі. Ми не обговорюємо тут їхню професійну кваліфікацію, але написання якісного тесту – завдання не з легких, яке потребує спеціальної підготовки. Тому змушена констатувати, що, на жаль, не всі матеріали, представлені на популярних українських онлайн-платформах тестування, мають належну якість, а тому вчителі повинні критично та педагогічно виважено використовувати кожну таку платформу. | ||
Після тестових платформ великою популярністю користуються також електронні підручники та відеоуроки (понад 60% респондентів), а також різноманітне прикладне програмне забезпечення (трохи менше 50% респондентів). Цікаво відзначити, що математичні програми на уроці використовують переважно ті, хто обирає комбінований підхід або працює онлайн (64% тих, хто обрав цей пункт). Тому можна вважати, що використання цього типу програмного забезпечення зручніше на онлайн-заняттях. | Після тестових платформ великою популярністю користуються також електронні підручники та відеоуроки (понад 60% респондентів), а також різноманітне прикладне програмне забезпечення (трохи менше 50% респондентів). Цікаво відзначити, що математичні програми на уроці використовують переважно ті, хто обирає комбінований підхід або працює онлайн (64% тих, хто обрав цей пункт). Тому можна вважати, що використання цього типу програмного забезпечення зручніше на онлайн-заняттях. | ||
| Рядок 39: | Рядок 64: | ||
Звісно, це не означає, що під час навчання рівень математичної підготовки студента не може підвищуватися. підготовка до ЗНО. Навпаки, будь-який спосіб підготовки до тестування спрямований на мобілізацію всіх можливих внутрішніх ресурсів випускника для успішного проходження цього тесту. Але основний акцент має бути на розвитку мислення та розширенні кругозору, а не на формальному заучуванні визначень, твердження та типові прийоми розв’язування вправ і задач. | Звісно, це не означає, що під час навчання рівень математичної підготовки студента не може підвищуватися. підготовка до ЗНО. Навпаки, будь-який спосіб підготовки до тестування спрямований на мобілізацію всіх можливих внутрішніх ресурсів випускника для успішного проходження цього тесту. Але основний акцент має бути на розвитку мислення та розширенні кругозору, а не на формальному заучуванні визначень, твердження та типові прийоми розв’язування вправ і задач. | ||
| − | Бажано, щоб учитель математики мав не одну визначену методику систематизації та повторення шкільної математики під час підготовки до ЗНО, а комплекс методик, які б дозволяли йому гнучко реагувати на особливості учнівської аудиторії та відповідати власним професійні схильності та уподобання. Належне використання ІКТ у цьому наборі методологій підготовки до ЗНО є природним саме по собі та в контексті пандемічної та карантинної ситуації останніх місяців. У зв’язку з цим важливою є належна підготовка вчителів до використання новітніх технологій як під час навчання в педагогічному університеті, так і в системі їх неперервної освіти. | + | Бажано, щоб учитель математики мав не одну визначену методику систематизації та повторення шкільної математики під час підготовки до ЗНО, а комплекс методик, які б дозволяли йому гнучко реагувати на особливості учнівської аудиторії та відповідати власним професійні схильності та уподобання. Належне використання ІКТ та ЕНК у цьому наборі методологій підготовки до ЗНО є природним саме по собі та в контексті пандемічної та карантинної ситуації останніх місяців. У зв’язку з цим важливою є належна підготовка вчителів до використання новітніх технологій як під час навчання в педагогічному університеті, так і в системі їх неперервної освіти. |
| − | Необхідна системна освітня програма для створення загальнодоступних методичних матеріалів щодо різних методів підготовки до ЗНО з математики, в тому числі з використанням | + | Необхідна системна освітня програма для створення загальнодоступних методичних матеріалів щодо різних методів підготовки до ЗНО з математики, в тому числі з використанням ЕНК. Цю програму, зокрема, можна реалізувати через мережу центрів та навчальних платформ, таких як «Освіторія», «Освіта.ua», «Всеосвіта», «НаУрок», GIOS та інші, а також через мережу центрів підвищення кваліфікації вчителів, зокрема онлайн-платформи. такі як Prometeus (www.prometheus.org.ua), Edera (www.ed-era.com), Coursera (www.coursera.org), Khan Academy (www.khanacademy.org), EdX (www.edx.org). ) тощо. |
'''СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ''' | '''СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ''' | ||
| Рядок 49: | Рядок 74: | ||
2. GIOS. (2021). Інтерактивні курси математики онлайн. Електронний ресурс, Режим доступу: https://gioschool.com. | 2. GIOS. (2021). Інтерактивні курси математики онлайн. Електронний ресурс, Режим доступу: https://gioschool.com. | ||
| − | 3. На Урок. (2021). Що здавати ЗНО. Електронний ресурс, Режим доступу: naurok.ua/student/blog/scho-take-zno | + | 3. Морзе Н.В. Критерії якості електронних навчальних курсів, розроблених на базі платформ дистанційного навчання / Н.В. Морзе, О.Г. Глазунова //Інформаційні технології в освіті. - Херсон: Херсонський державний університет. - 2009. - Випуск 4. -С . 6 3 – 75. |
| + | |||
| + | 4. На Урок. (2021). Що здавати ЗНО. Електронний ресурс, Режим доступу: https://naurok.ua/student/blog/scho-take-zno. | ||
| + | |||
| + | 5. Освіторія. (2021). Як карантин змінюють наших дітей: розповідають вчителі. Електронний ресурс, Режим доступу: https://osvitoria.media/experience/yak-karantyn-zminyuye-nashyh-ditej-rozpovidayut-vchyteli/. | ||
| − | + | 6. Освіторія. (2021). Найбільше дітей відстають в математиці: як закриття школи вплинуло на учнів? Електронний ресурс, Режим доступу: https://osvitoria.media/experience/doslidzhennya-yak-pandemiya-vplynula-na-shkolyariv/. | |
| − | + | 7. Положення про атестацію електронного навчального курсу на рівні ВНЗ та МОН України. www.mon.gov. ua/images/gr/obg/2010/08_06_10.pdf | |
| − | + | 8. Рейтингова група Україна. (2018). Динаміка ставлення українців до ЗНО / О.В. Електронний ресурс, Режим доступу: http://ratinggroup.ua/research/ukraine/dinamika_otnosheniya_ukraincev_k_vno_zno.html. | |
| − | + | 9. Роганін О. М. (2020). ЗНО 2021. Математика. Збірник тестових завдань / ЗНО 2021. Математика. Збірник тестових завдань. | |
| − | + | 10. Школьний О. В. (2021). Що таке ЗНО з чим його «їдять»? Електронний ресурс, Режим доступу: https://www.blog.gioschool.com/zno2. | |
| − | + | 11. Школьний О., Тихоненко Ю. (2021). Доцільність та можливість використання ІКТ під час підготовки до ЗНО з математики. Фізико-математична освіта. Випуск 2(28). Р. 11-16. | |
| − | + | 12. Школьний О.В., Захарійченко Ю.В. О. (2020). Сучасна тематична підготовка до ЗНО з математики в Україні: координати та вектори, елементи комбінаторики та стохастики. Фізико-математичне виховання. Випуск 1 (23). С.171-176. | |
| − | + | 13. Школьний О.В., Захарійченко Ю.В. О. (2020). Методичні поради щодо підготовки до ЗНО з математики в сучасних умовах. Фізико-математичне виховання. Випуск 3 (25). С. 6-10. | |
Поточна версія на 17:43, 25 травня 2023
Використання ЕНК на уроках математики як засобу підготовки до ЗНО
Постановка проблеми. Організація дистанційного навчання для здобувачів освіти в Україні набула особливого значення у зв’язку з викликами, що поставили перед українським суспільством спочатку пандемія Сovid-19, а останні півроку російсько-українська війна. Вже три роки навчання в Україні, а отже, значна частина життя перейшла в цифровий світ. ІКТ, ЕНК, сучасні е-ресурси, інтернет мережа надають можливість проводити навчальний процес, зокрема допомагати у підготовці до ЗНО, при цьому не втрачаючи якості навчання.
Не викликає сумнівів актуальність удосконалення методики підготовки до зовнішнього незалежного оцінювання (ЗНО) навчальних досягнень українських випускників. Цей тип національного стандартизованого оцінювання в Україні постійно перебуває у центрі уваги як фундаментальних досліджень (див. (Дворецька, 2015), (Ляшенко та Раков, 2008), (Іяковлєва та Каплун, 2019) та ін.), так і публікацій у ЗМІ (див. (Рейтинг Груп Україна, 2018), (НаУрок, 2021), (Швадчак, 2021) тощо).Водночас ставлення до ЗНО загалом і до ЗНО з математики зокрема в українському суспільстві в цілому позитивне.
Наприклад, опитування понад 700 користувачів (учнів, їхніх батьків та вчителів математики) освітньої платформи GIOS [2] показує, що середній бал якості ЗНО з математики в Україні за 10-бальною шкалою (1 – найнижчий рівень задоволеності, 10 – найвищий) дорівнює 7, а найпопулярніше значення цієї якості – 8. Серед найбільших переваг незалежного оцінювання часто називають: зменшення корупції під час вступу до університетів (42% респондентів), можливість об’єктивно оцінити рівень навчальних досягнень учнів з математики (28%), можливість ширшого вибору навчальних закладів під час вступної кампанії (26%) та підвищення престижу вивчення математики в школі (18). %).
Сильним стимулом для розвитку ІКТ у навчанні математики також стала нинішня воєнна та попередня пандемічна ситуація, коли запровадження карантину та тривалі періоди онлайн-навчання вже сприймаються і учнями, і вчителями як цілком нормальні навчальні ситуації. За цих обставин вчителі та репетитори математики часто просто змушені використовувати ІКТ, створювати та розвивати нові форми організації навчального процесу, удосконалювати та відповідно адаптувати методики та технології навчання.
Мета статті: з’ясувати доцільність використання ЕНК, а також як місце і роль технологій у підготовці до ЗНО з математики з позиції тих, хто цю підготовку здійснює (вчителів, репетиторів тощо); визначити, наскільки сучасні технології сприяють чи перешкоджають пошуку оптимальних методів підготовки до незалежного тестування з математики; окреслити шляхи розробки методичних рекомендацій щодо використання ЕНК при підготовці до ЗНО з математики.
Матеріали та методи дослідження Для досягнення поставленої мети використано теоретичний метод аналізу методичної літератури з досліджуваного питання. Також я використовую деякі емпіричні методи: власне опитування за допомогою електронного інструменту Google form, спостереження за навчальним процесом у загальноосвітніх школах та на курсах підготовки до спеціальних іспитів, а також аналіз досягнень учнів. У цій статті я також використовую комплекс методів наукового пізнання: порівняльний аналіз для з’ясування різних поглядів на проблему та визначення напрямків дослідження; систематизація та узагальнення з метою висновків і формулювання рекомендацій щодо підготовки до загальнодержавного стандартизованого оцінювання навчальних досягнень з математики; узагальнення педагогічного досвіду та спостережень.
Виклад основного матеріалу У ЗНО з математики передбачається перевірка навчальних досягнень випускників з програмового матеріалу за 5 - 11 класи. Така перевірка використовує педагогічний тест. Згідно з [7] «педагогічний тест ... – це набір завдань з певної галузі знань (навчального предмета), побудованих за певними правилами викладу умови і надання відповіді, за допомогою яких оцінюється рівень навчальних досягнень учнів (знання, вміння, предметна компетентність тощо)».
Хоча педагогічне тестування має багато недоліків, але воно дає змогу:
• перевірити результати навчальних досягнень водночас із багатьох тем і розділів програми;
• об’єктивно оцінити рівень засвоєння навчального матеріалу;
• створити для всіх учасників тестування рівні умови складання тестів;
• стандартизувати та автоматизувати процедуру перевірки результатів;
• охопити тестуванням велику кількість учнів [3].
Зрозуміло, що не існує універсальної методики підготовки до ЗНО з математики, яка б гарантувала високий бал кожному учаснику тестування. Дійсно, це суттєво залежить від студентської аудиторії та індивідуальних особливостей викладача чи репетитора, який його здійснює. Перш за все, слід говорити про комплекс методів, які дозволять сучасному вчителю математики досягти бажаного результату, який, у свою чергу, залежить від мети підготовки до ЗНО. Зупинимося на цьому питанні докладніше.
На мою думку, незалежне оцінювання є лише інструментом адекватного оцінювання рівня навчальних досягнень учнів, своєрідною «лінійкою», яка призначена лише для «вимірювання» і не більше того. Для мене також очевидно, що ЗНО з математики чи будь-якого іншого предмету не має бути метою шкільного навчання. Головною метою навчання в школі є розвиток дитини, виявлення і розкриття її здібностей, а також формування тих життєвих компетентностей, які дозволять їй у майбутньому знайти своє місце в житті, реалізуватися як особистості. І незалежне тестування, хоч і є класичним «високим тестуванням» [11], саме по собі не може стати кінцевою метою чи викладання кожної дисципліни, чи навіть вказівка до створення методики навчання.
Тому я вважаю, що основною метою вчителя при підготовці до ЗНО з математики є повторення та систематизація даних зі шкільного курсу математики, а не формальне привчання учнів до цілком конкретних класів тестових завдань. Звичайно, необхідно адаптувати випускників до особливостей розв’язування тестових завдань різної форми (з альтернативою, з короткою відповіддю, на встановлення відповідності, з повним поясненням), але ця мета є другорядною і не може витіснити чи замінити основну.
Також важливою при підготовці до ЗНО з математики є мета, яку ставить перед собою майбутній учасник цього ЗНО. З першого погляду видно, що студент хоче набрати якомога більше балів. Однак такий підхід може мати серйозні негативні наслідки в майбутньому. На мою думку, більш природним є те, що учні під час підготовки до ЗНО намагаються отримати не максимальний, а «свій» бал, тобто такий, який адекватно відображатиме реальний рівень підготовки і дозволить здавати «своє» місце за обраною спеціальністю в університеті. Таке цілепокладання дозволить випускнику уникнути значних психологічних проблем під час підготовки до тестування, а також з часом знайти ту спеціальність і університет, які дозволять йому стати реалізованою та щасливою людиною (детальніше про це див. у статті [10, 11].
Після узгодження цілей підготовки до ЗНО для учня та вчителя природним наступним кроком є вибір відповідної методики систематизації та повторення шкільної математики. Як уже зазначалося, цей вибір залежить від багатьох факторів, але сьогодні, після більш ніж 15-річної історії, набір таких методик уже сформовано та відображено в різних посібниках для підготовки до незалежного оцінювання ((Бевз та Буковська, 2020), (Гальперіна, 2020), (Капіносов, 2020), (Нелін, 2016), (Роганін, 2020), (Захарійченко та ін., 2020), Захарійченко та ін., 2021)). Кожна з цих книг має свою внутрішню логіку, послідовність вивчення тем, свої переваги та недоліки.
Наступним кроком після вибору відповідної методики є підбір засобів навчання, а також вибір зручних для студента та викладача організаційних форм цього навчання. До 2020 року традиційно найпопулярнішим засобом підготовки до ЗНО з математики є друкований підручник, а найпопулярнішими організаційними формами – групові або індивідуальні заняття в класі. Як додаткові засоби навчання використовувалися різноманітні роздаткові матеріали, зокрема навчальні тематичні та комбіновані контрольні роботи, що містять завдання різної форми. Також популярними були навчальні онлайн-тести, зокрема тести ЗНО минулих років.
Однак у зв’язку з пандемічною ситуацією та запровадженням карантину після 2020 року ситуація суттєво змінилася, оскільки заняття в аудиторіях стали неможливими. Студентам і викладачам довелося фактично терміново освоювати засоби дистанційного спілкування (Google Meet, Skype, Zoom та ін.) та платформи для дистанційного та змішаного навчання (Google Classroom, MS Teams, MOODLE, НаУрок та ін.), з за допомогою якого, зокрема, проводились і контрольні заходи у формі комп’ютерного тестування.
Описана ситуація призвела до суттєвих змін у сприйнятті ІКТ як студентами, так і викладачами та викладачами. Це підтверджують результати вищезгаданого опитування користувачів освітньої платформи GIOS [2], серед яких 49% респондентів обрали найбільш оптимальним способом підготовки до ЗНО з математики спосіб занять з репетитором за друкованими посібниками. та онлайн-платформи. Проте це опитування не заглиблювалося в деталі та особливості використання вчителями та репетиторами новітніх технологій під час підготовки до ЗНО з математики. Тому я провела власне опитування вчителів математики щодо використання ними ЕНК під час підготовки учнів до незалежного оцінювання.
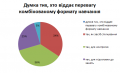
Згідно результатів досліження, серед респондентів більше 80% беруть безпосередню участь у підготовці учнів до ЗНО з математики, решта – опосередковано. Дві третини респондентів вважають, що найкращим способом підготовки до ЗНО сьогодні є поєднання аудиторних занять та онлайн-формату. Водночас майже третина вважає, що таке навчання має здійснюватися виключно в аудиторії. Виключно онлайн-формат підготовки до тестування не є популярним з точки зору його ефективності та ефективності. Можна припустити, що перевага на користь комбінованого підходу (аудиторний формат та онлайн-заняття) є наслідком вимушеного активного розвитку та практичного застосування змішаного навчання протягом останнього року. Відповідно, якщо за таких умов роботи та навчання студенти будуть показувати не нижчі результати, ніж за класичних форм роботи, то, швидше за все, ми побачимо ще більший відсоток прихильників комбінованого підходу. Однак можлива й зворотна ситуація, коли перехід від аудиторної роботи до онлайн не виправдає своєї ефективності в очах її нинішніх прихильників
Зазначу, що 98% респондентів вважають використання ЕНК доцільним під час підготовки до ЗНО з математики. Так званим «лідером використання» новітніх технологій є онлайн-платформи для тестування (близько 80% респондентів). Причому цей показник приблизно однаковий як серед тих, хто вважає ефективнішим комбінований підхід у навчанні, так і серед тих, хто вважає більш ефективним лише аудиторне навчання. Тобто онлайн-тестування активно використовується і під час роботи на уроці. Також 45% прихильників аудиторного формату навчання та 54% тих, хто обирає комбінований підхід, вважають за доцільне використовувати ІКТ під час підготовки до уроків.
Цікаво відзначити, що відсоток тих, хто використовує ЕНК для спілкування зі студентами, більш ніж утричі вищий серед тих, хто використовує комбінований підхід, ніж серед тих, хто надає перевагу суто аудиторній роботі. При цьому відсоток тих, хто не має технічної можливості правильно використовувати можливості ЕНК, також втричі вищий серед тих, хто вважає навчання в аудиторному форматі ефективнішим. Таким чином, на прихильність до включення онлайн-формату в процес підготовки до ЗНО з математики значною мірою впливає технічне забезпечення викладача, зокрема, в контексті можливості спілкування зі студентом без живих зустрічей.
Як видно з рисунку 2, серед усіх сучасних технологій, які використовують вчителі математики під час підготовки до ЗНО з математики, лідирують платформи онлайн-тестів (їми користуються майже 80% респондентів). Однак найбільшою проблемою цих платформ є низький рівень рецензування та перевірки їхніх матеріалів, оскільки переважну більшість тестів на цих платформах пишуть самі викладачі. Ми не обговорюємо тут їхню професійну кваліфікацію, але написання якісного тесту – завдання не з легких, яке потребує спеціальної підготовки. Тому змушена констатувати, що, на жаль, не всі матеріали, представлені на популярних українських онлайн-платформах тестування, мають належну якість, а тому вчителі повинні критично та педагогічно виважено використовувати кожну таку платформу.
Після тестових платформ великою популярністю користуються також електронні підручники та відеоуроки (понад 60% респондентів), а також різноманітне прикладне програмне забезпечення (трохи менше 50% респондентів). Цікаво відзначити, що математичні програми на уроці використовують переважно ті, хто обирає комбінований підхід або працює онлайн (64% тих, хто обрав цей пункт). Тому можна вважати, що використання цього типу програмного забезпечення зручніше на онлайн-заняттях.
Серед конкретних електронних ресурсів, які використовуються в роботі учасників опитування, відзначимо тестові платформи На Урок (www.naurok.ua/student/tests), Освіта.ua (www.osvita.ua), Всеосвіта (www.vseosvita.ua), Quizlet (www.quizlet.com) та Classtime (www.classtime.com), а також сайти з тестами ЗНО минулих років (www.zno.osvita.ua/mathematics/).
Висновки На мою думку, найважливішим як для вчителя, так і для учня при підготовці до ЗНО з математики є забезпечення належної якості систематизації шкільного курсу математики, а не формальна підготовка до розв’язування конкретних класів тестових завдань. Надзвичайно важливо, щоб вчителі та учні усвідомили необхідність у жодному разі не отримати максимально можливий бал під час тестування, а визначити їхній реальний рівень математичної підготовки. Це сприятиме подальшому успішному навчанню випускника у ВНЗ та його подальшій реалізації як фахівця, так і як особистості.
Звісно, це не означає, що під час навчання рівень математичної підготовки студента не може підвищуватися. підготовка до ЗНО. Навпаки, будь-який спосіб підготовки до тестування спрямований на мобілізацію всіх можливих внутрішніх ресурсів випускника для успішного проходження цього тесту. Але основний акцент має бути на розвитку мислення та розширенні кругозору, а не на формальному заучуванні визначень, твердження та типові прийоми розв’язування вправ і задач.
Бажано, щоб учитель математики мав не одну визначену методику систематизації та повторення шкільної математики під час підготовки до ЗНО, а комплекс методик, які б дозволяли йому гнучко реагувати на особливості учнівської аудиторії та відповідати власним професійні схильності та уподобання. Належне використання ІКТ та ЕНК у цьому наборі методологій підготовки до ЗНО є природним саме по собі та в контексті пандемічної та карантинної ситуації останніх місяців. У зв’язку з цим важливою є належна підготовка вчителів до використання новітніх технологій як під час навчання в педагогічному університеті, так і в системі їх неперервної освіти.
Необхідна системна освітня програма для створення загальнодоступних методичних матеріалів щодо різних методів підготовки до ЗНО з математики, в тому числі з використанням ЕНК. Цю програму, зокрема, можна реалізувати через мережу центрів та навчальних платформ, таких як «Освіторія», «Освіта.ua», «Всеосвіта», «НаУрок», GIOS та інші, а також через мережу центрів підвищення кваліфікації вчителів, зокрема онлайн-платформи. такі як Prometeus (www.prometheus.org.ua), Edera (www.ed-era.com), Coursera (www.coursera.org), Khan Academy (www.khanacademy.org), EdX (www.edx.org). ) тощо.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Бевз,В. Х., Буковська,О. І. (2020). Математика: Тестові завдання у форматі ЗНО. Математика: Тестові завдання у форматі ЗНО.
2. GIOS. (2021). Інтерактивні курси математики онлайн. Електронний ресурс, Режим доступу: https://gioschool.com.
3. Морзе Н.В. Критерії якості електронних навчальних курсів, розроблених на базі платформ дистанційного навчання / Н.В. Морзе, О.Г. Глазунова //Інформаційні технології в освіті. - Херсон: Херсонський державний університет. - 2009. - Випуск 4. -С . 6 3 – 75.
4. На Урок. (2021). Що здавати ЗНО. Електронний ресурс, Режим доступу: https://naurok.ua/student/blog/scho-take-zno.
5. Освіторія. (2021). Як карантин змінюють наших дітей: розповідають вчителі. Електронний ресурс, Режим доступу: https://osvitoria.media/experience/yak-karantyn-zminyuye-nashyh-ditej-rozpovidayut-vchyteli/.
6. Освіторія. (2021). Найбільше дітей відстають в математиці: як закриття школи вплинуло на учнів? Електронний ресурс, Режим доступу: https://osvitoria.media/experience/doslidzhennya-yak-pandemiya-vplynula-na-shkolyariv/.
7. Положення про атестацію електронного навчального курсу на рівні ВНЗ та МОН України. www.mon.gov. ua/images/gr/obg/2010/08_06_10.pdf
8. Рейтингова група Україна. (2018). Динаміка ставлення українців до ЗНО / О.В. Електронний ресурс, Режим доступу: http://ratinggroup.ua/research/ukraine/dinamika_otnosheniya_ukraincev_k_vno_zno.html.
9. Роганін О. М. (2020). ЗНО 2021. Математика. Збірник тестових завдань / ЗНО 2021. Математика. Збірник тестових завдань.
10. Школьний О. В. (2021). Що таке ЗНО з чим його «їдять»? Електронний ресурс, Режим доступу: https://www.blog.gioschool.com/zno2.
11. Школьний О., Тихоненко Ю. (2021). Доцільність та можливість використання ІКТ під час підготовки до ЗНО з математики. Фізико-математична освіта. Випуск 2(28). Р. 11-16.
12. Школьний О.В., Захарійченко Ю.В. О. (2020). Сучасна тематична підготовка до ЗНО з математики в Україні: координати та вектори, елементи комбінаторики та стохастики. Фізико-математичне виховання. Випуск 1 (23). С.171-176.
13. Школьний О.В., Захарійченко Ю.В. О. (2020). Методичні поради щодо підготовки до ЗНО з математики в сучасних умовах. Фізико-математичне виховання. Випуск 3 (25). С. 6-10.